MATEMÁTICAS

¿Que es la segunda deribada?

La derivada de una función matemática es la velocidad de cambio de una función en un determinado punto cuando su variable independiente cambia.

También se define como el límite de la razón de cambio instantanea que sufre la variable independiente, al establecerse un incremento a la variable independiente positivo o negativo, y este incremento lo aproximamos a cero.

La segunda derivada de una función f mide la concavidad de la gráfica de f. Una función cuya segunda derivada es positiva será cóncava hacia arriba (también conocida como convexa), lo que significa que la línea tangente estará debajo de la gráfica de la función. De manera similar, una función cuya segunda derivada es negativa será cóncava hacia abajo (también llamada simplemente cóncava), y sus líneas tangentes estarán sobre la gráfica de la función.

¿PORQUE LA SEGUNDA DERIVADA INDICA LA CONCAVIDAD?

• Cuando f(x)>0, significa que la pendiente f'(z) está aumentando. Esto ocurre cuando la curva de f(x) está "abriéndose hacia arriba o tiene una forma de taza, lo cual indica concavidad hacia arriba.
  
• Cuando f"(z) <0, significa que la pendiente f'(z) está disminuyendo. Esto ocurre cuando la curva de f(z) se "cierra hacia abajo" o tiene forma de montaña, lo cual indica convexidad hacia arriba.

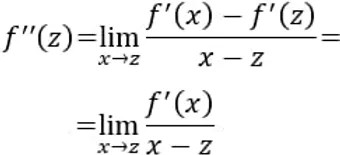
APLICACIÓN DE LA SEGUNDA DERIBADA:

La segunda derivada de una función tiene múltiples aplicaciones en diversas áreas, podemos observar algunas de ellas a continuación:

• Concavidad y Convexidad de Funciones:

La segunda derivada ayuda a determinar si una función es cóncava hacia arriba o cóncava hacia abajo en un intervalo específico.

Si , la función es cóncava hacia arriba (forma de "U"), y si , es cóncava hacia abajo (forma de "n"). Esta información es importante para entender el comportamiento de una función en términos de crecimiento y disminución.

2. Identificación de Puntos de Inflexión:

Un punto de inflexión ocurre cuando la función cambia de concavidad, lo cual puede indicarse cuando y la concavidad cambia a ambos lados del punto.

Los puntos de inflexión son clave en el análisis de gráficos y funciones, ya que marcan transiciones en la forma de la curva.

3. Optimización y Clasificación de Extremos:

La segunda derivada es utilizada en el criterio de la segunda derivada para clasificar los puntos críticos de una función:

• Si en el punto crítico, el punto es un mínimo local.
  
• Si , el punto es un máximo local.

Esto es útil en problemas de optimización, ya que permite encontrar los puntos de máximo o mínimo de una función en un intervalo, como el costo mínimo o el beneficio máximo en aplicaciones económicas.

4. Física y Movimiento:

En cinemática, la segunda derivada de la posición con respecto al tiempo da la aceleración de un objeto.

Esto permite analizar el cambio en la velocidad de un objeto en movimiento y predecir su comportamiento, lo cual es fundamental en el estudio de trayectorias, dinámica y fuerzas.

5. Ingeniería y Análisis Estructural:

En ingeniería, la segunda derivada se utiliza en el análisis de la curvatura de vigas y otros elementos estructurales.

La curvatura ayuda a evaluar la resistencia y flexibilidad de materiales, prediciendo puntos de posible falla y optimizando el diseño de estructuras para que soporten mejor las cargas y tensiones.

6. Economía y Finanzas:

En economía, la segunda derivada se usa para evaluar la sensibilidad de una variable (como el costo o la demanda) frente a cambios de otra variable (como el precio).

También permite identificar puntos de máximo beneficio o mínimo costo y analizar la rapidez con la que cambia la tasa de crecimiento de una variable, lo que es útil para tomar decisiones estratégicas.

REGLAS CON LA SEGUNDA DERIVADA

1. Concavidad de la Función

• Si f{\prime}{\prime}(x) > 0 en un intervalo, la función f(x) es convexa o cóncava hacia arriba en ese intervalo. Esto significa que la curva se abre hacia arriba, y las tangentes a la curva tienen una pendiente creciente.

• Si f{\prime}{\prime}(x) < 0 en un intervalo, la función f(x) es cóncava o cóncava hacia abajo en ese intervalo. En este caso, la curva se abre hacia abajo, y las tangentes a la curva tienen una pendiente decreciente.

2. Puntos de Inflexión

• Un punto de inflexión es un punto en el cual la concavidad de la función cambia de cóncava hacia arriba a cóncava hacia abajo, o viceversa.

• Para que haya un punto de inflexión en x = a :

• La segunda derivada en ese punto debe cambiar de signo (de positiva a negativa o de negativa a positiva) en torno a x = a .

• Puede ser que f{\prime}{\prime}(a) = 0 en este punto, pero no siempre. En algunos casos, la segunda derivada no es cero en el punto de inflexión, pero sí cambia de signo.

3. Segunda Derivada y Máximos/Mínimos Relativos (Prueba de la Segunda Derivada)

• La segunda derivada se puede usar para confirmar si un punto crítico x = a (donde f{\prime}(a) = 0 ) es un máximo o mínimo relativo.

• Si f{\prime}{\prime}(a) > 0 , entonces f(x) tiene un mínimo relativo en x = a .

• Si f{\prime}{\prime}(a) < 0 , entonces f(x) tiene un máximo relativo en x = a .

• Si ( f''(a) = 0 o no existe**, la prueba de la segunda derivada es inconclusa, y se debe utilizar otro método, como la prueba de la primera derivada o el análisis de la concavidad.

EJERCICIO 1: Funcion Convexa (convacidad hacia arriba)

Consideremos la función f(x) = x^3 + 3x^2 + 5 .

Paso 1: Derivar la función

Primero encontramos la primera derivada de f(x) :

f{\prime}(x) = 3x^2 + 6x

Paso 2: Calcular la segunda derivada

Ahora, derivamos nuevamente para encontrar la segunda derivada de f(x) :

f{\prime}{\prime}(x) = 6x + 6

Paso 3: Determinar la concavidad

La concavidad se determina observando el signo de f{\prime}{\prime}(x) :

• Si f{\prime}{\prime}(x) > 0 , la función es convexa o cóncava hacia arriba.

• Si f{\prime}{\prime}(x) < 0 , la función es cóncava o cóncava hacia abajo.

En este caso, f{\prime}{\prime}(x) = 6x + 6 . Vamos a analizar el signo de f{\prime}{\prime}(x) :

• Para x > -1 , f{\prime}{\prime}(x) > 0 , lo que indica que f(x) es convexa (cóncava hacia arriba).

• Para x < -1 , f{\prime}{\prime}(x) < 0 , lo que indica que f(x) es cóncava (cóncava hacia abajo).

Por lo tanto, la función es convexa para valores de x > -1 , y cóncava para x < -1 .

EJERCICIO 2: Funcion Cóncava (Concavidad hacia Abajo)

Consideremos la función g(x) = -2x^2 + 4x + 3 .

Paso 1: Derivar la función

Primero, encontramos la primera derivada de g(x) :

g{\prime}(x) = -4x + 4

Paso 2: Calcular la segunda derivada

Derivamos nuevamente para obtener la segunda derivada de g(x) :

g{\prime}{\prime}(x) = -4

Paso 3: Determinar la concavidad

En este caso, la segunda derivada g{\prime}{\prime}(x) = -4 es constante y negativa para todo valor de x . Esto implica que la función es siempre cóncava (cóncava hacia abajo).

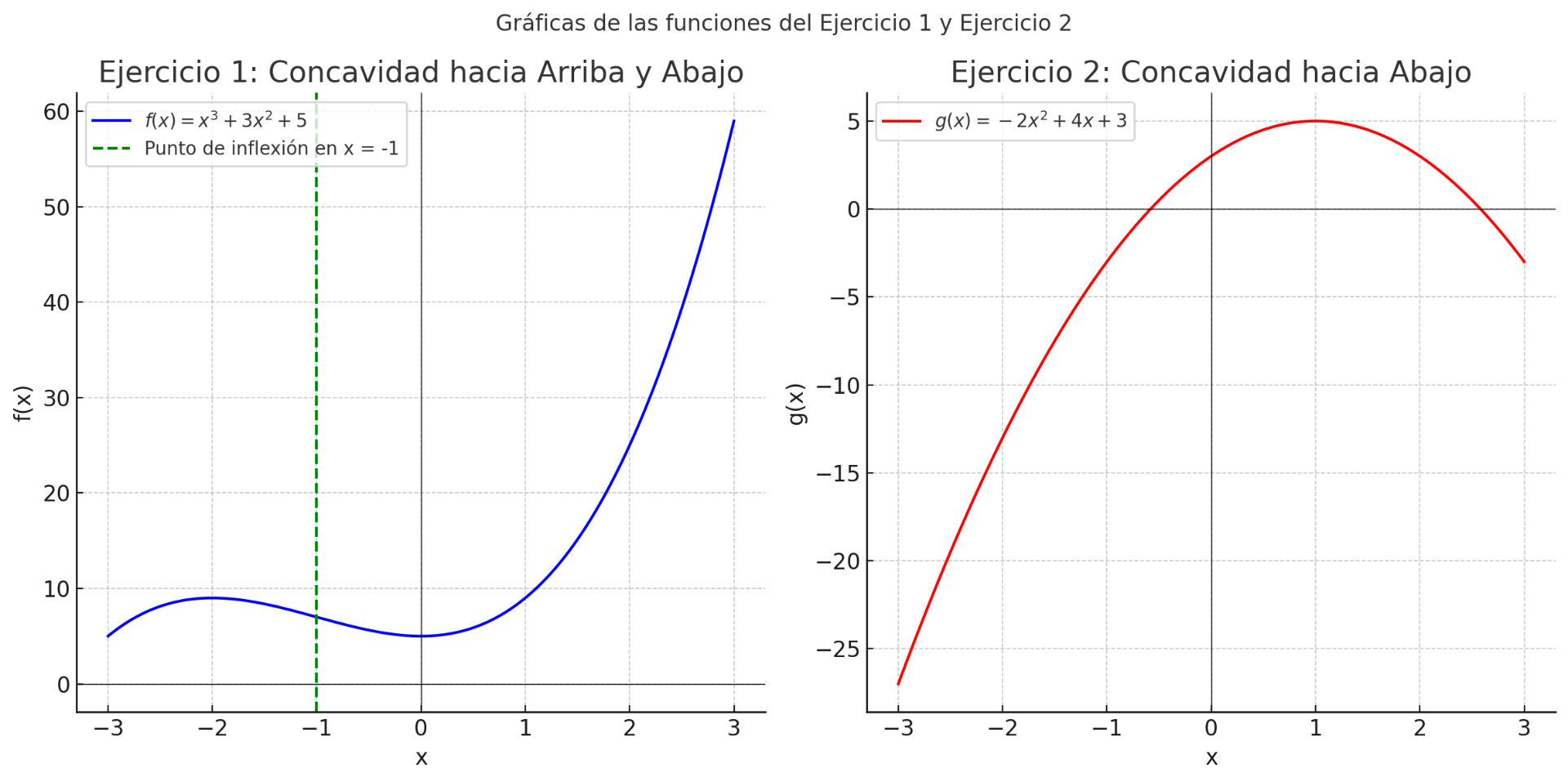
CONCLUSIÓN:

En el primer ejemplo, la función f(x) = x^3 + 3x^2 + 5 muestra regiones de concavidad hacia arriba y hacia abajo dependiendo del intervalo de x . En el segundo ejemplo, la función g(x) = -2x^2 + 4x + 3 es cóncava hacia abajo en todo su dominio. Estos ejercicios ilustran cómo la segunda derivada permite analizar y justificar la concavidad de una función en términos de su forma y comportamiento.